Spintronics and topological phases of matter
Dr. A. Matos-Abiague's group is focused on the theoretical investigation of spin-dependent phenomena in condensed matter systems and their potential applications in spintronics (spin electronics) and quantum computing. The main research topics in our group are described below.
Spintronics
Spintronics is an alternative to conventional electronics in which not only the charge but also the intrinsic magnetic moment (spin) of the carriers can be used for both memory and logic operations. Since the manipulation of spins can be performed faster and with less energy than required for manipulating electric charge, sprintronics promises to provide devices with improved performance and less power consumption.
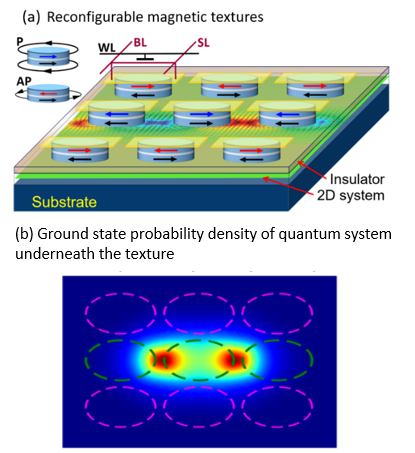
Our research combines analytical and numerical simulations to uncover new spin-dependent phenomena in two-dimensional crystals and hybrid heterostructures comprising semiconductors, superconductors, and ferromagnets. Controlling the spin of the carriers allows for tuning optical and transport properties of materials. The spin-orbit coupling (SOC) is an interaction that couples spin and momentum to electric fields. This allows for spin and transport control by electric means. The SOC in isolated atoms is fairly small, but its strength can be effectively enhanced by several orders of magnitude in properly designed heterostructures. This paves the way for using the SOC for electric control of novel spintronic devices.
The tunability of the symmetry and strength of the spin-orbit fields is limited because it is mostly determined by the atomic structure of the system. However, spin-orbit fields can effectively be created by using magnetic textures produced by arrays of spin-valve nanomagnets acting on nearby electron (or hole) system. This, so-called synthetic SOC can be locally controlled at the nanometric scale by reconfiguring the fringe fields of the magnetic array, providing new opportunities for designing and manipulating quantum states on demand. Our group performs micromagnetic simulations combined with quantum mechanical calculations to explore new phenomena emerging in such reconfigurable systems.
Review articles:
Topological phases of matter
The fragility of conventional quantum bits (qubits) requires the implementation of massive quantum error correction. This could be mitigated by using topological qubits, which are robust against local perturbations and less prone to errors. We conduct research on the properties of topological phases of matter (e.g., topological insulators, topological superconductivity) with particular interest in the design, emergence, control, and detection of the topological superconducting phase, and its potential use for building topologically protected quantum bits (qubits). The group maintains a strong collaboration with Prof. I. Zutic's group (SUNY at Buffalo) and Prof. J. Shabani's group (New York University).
Quantum computing
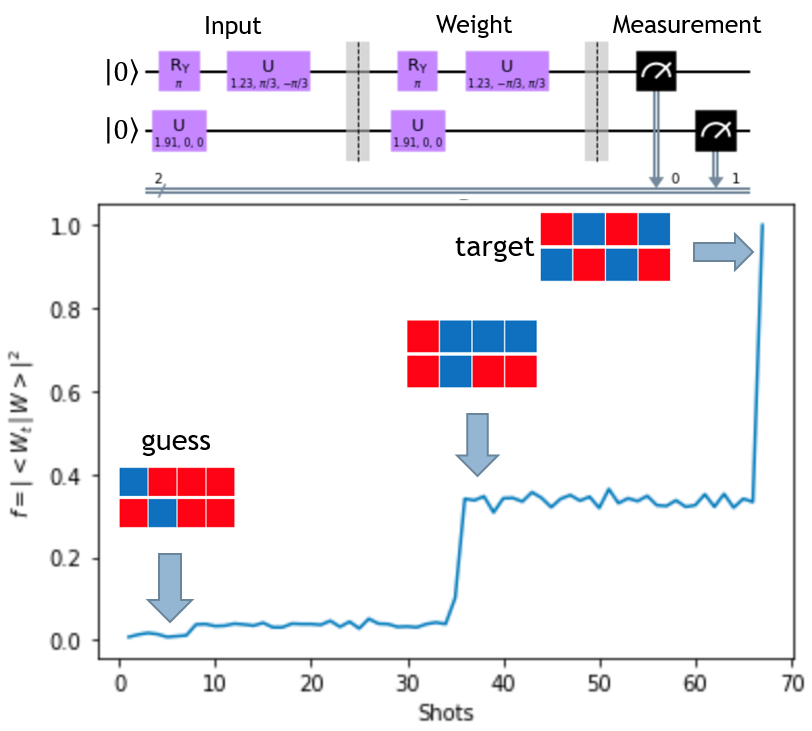
Bottom: Training of a quantum perceptron.
After 68 training steps the perceptron learned to
recognize a target pattern.
Artificial intelligence and quantum computing will arguably have the largest transformative effects not only on our daily lives but also on scientific research in the next decades. The combination of those two emergent technologies will revolutionize science by making possible to deal with biological, chemical, and physical systems whose high complexity cannot be treated by standard methods nor conventional computers. Unlike conventional computers, which use bits, quantum computers use quantum bits (qubits). Qubits provide an intrinsic parallelism because, if in a superposition, they can be in two different states (0 and 1) simultaneously. This leads to an impressive increase of computational power with respect to a classical computer. Our group is working in collaboration with Prof. L. Candelori's group (Department of Mathematics) to design quantum algorithms that take advantage of the increased encoding power of qubits and the intrinsic parallelism for improving the performance and training times of quantum neurons in tasks such as pattern recognition.
Recent publications:
T. Zhou, M. C. Dartiailh, K. Sardashti, J. E. Han, A. Matos-Abiague, J.Shabani, and Igor Zutic. Fusion of Majorana bound states with mini-gate control in two-dimensional systems, Nature Communications 13, 1738 (2022).
B. Pekerten, J. D. Pakizer, B. Hawn, and A. Matos-Abiague. Anisotropic topological superconductivity in Josephson junctions, Physical Review B 105, 054504 (2022).
J. D. Pakizer and A Matos-Abiague. Signatures of topological transitions in the spin susceptibility of Josephson junctions, Physical Review B 104, L100506 (2021).
J. D. Pakizer and A Matos-Abiague. Crystalline anisotropic topological superconductivity in planar Josephson junctions , Physical Review Research B 3, 013198 (2021).
M. C. Dartiailh, W. Mayer, J. Yuan, K. S. Wickramasinghe, A. Matos-Abiague, I. Zutic, and J. Shabani. Phase signature of topological transition in Josephson junctions, Physical Review Letters 126, 036802 (2021).