Quantum transport and low-temperature physics research
Strongly correlated many-body quantum systems
The study of the many-body electron systems encompasses two of the most fundamental subjects: electron-electron interaction and electron-disorder interaction.
It is well known that sufficient disorder causes electron states to undergo Anderson Transition. On the other hand, whether strong electron-electron interaction also brings radical changes, such as the predicted Wigner Crystallization (electron solid), is still unknown. For a long time, experimental effort was hindered because most devices contain a high level of unwanted disorder which overwhelms the interaction effect at low electron densities.
Recent breakthroughs have been made in providing ultra-high quality two-dimensional electron systems in GaAs semiconductor field-effect transistors. The following projects will utilize this type of devices with record low electron densities to perform transport experiments at low temperatures. The goal is to verify whether strong electron-electron interaction drives a first-order phase transition (Wigner crystallization) or some intermediate phases.
Either observation will provide insights into understanding the quantum mechanical nature of strongly interacting electrons in the form of a solid or a strongly correlated liquid.
Projects
Interaction-driven in high-purity two-dimensional systems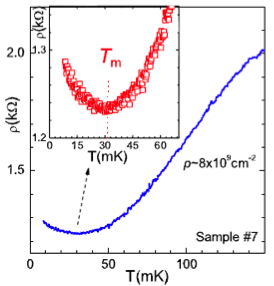 
Following the seminal work of Anderson Localization, the scaling theory of localization (STL) predicted there are no 2D metallic ground states for non-interacting particles. Whether strong electron-electron interaction can modify the statement is fundamentally important.
The consequently observed 2D metal-to-insulator transition (MIT) indeed suggests a complex disorder-interaction interplay that is still not well understood. Utilizing the high purity 2D hole systems. Our measurement in the metallic side of MIT exhibits the onset of an insulating behavior (figure on right). The origin of this behavior is being investigated as a possible Condon effect or something else.
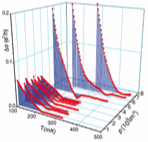On the other hand, the measurement on the insulating side reveals a non-activated conduction, qualitatively different than the usual hopping behavior of an Anderson insulator. Moreover, conductivity kinks have been observed in the temperature dependence of the conductivity (figure on left) for rs > 40. This discontinuity could indicate a phase transition driven by the increasing interaction effects.
Strongly correlated one-dimensional systems
The 2D hole systems of ultra-low charge densities realized in HIGFETs have a profound impact on electron physics research on nanoscales. A charge concentration of 6 × 102 cm-2 corresponds to an average charge spacing of 0.5 µm and a nominal Fermi wavelength of 1 µm. Compared to the extremely demanding resolution for fabricating less than 20-30nm wide single-mode wires in high-density devices, the single-mode can be easily realized in HIGFETs with a wire of 300 - 500 nm wide.
Moreover, the enormous average charge spacing also provides the precious room for implementing nanoprobes between individual charges and performing charge and spin manipulation at a single particle level. In 1D HIGFET dilute systems, the interaction is further enhanced due to the reduced dimensionality (rs = me2/p2hε), more prominent than in the 2D scenario. Lowering the charge density is expected to drive the state from a Luttinger liquid, where electrons are extended over the length of the wire, to a Wigner crystal, where the electrons are spatially separated, by the long-range Coulomb interaction.
Even though the 1D Wigner crystal was recently observed in Carbon nanotubes, a transition from liquid to crystal has not been demonstrated. Important questions on the nature of the transition and how it occurs remain unanswered. The advantage of utilizing the HIGFETs is that a huge range of interaction is covered as the average charge spacing can be tuned up to five times of that in the nanotubes. In the meantime, the disorder level is much lower. Therefore, the HIGFET systems are more suitable for capturing the expected phase transition.
For more information on this research, see Jian Huang's research.